Acronyms are generally scary, and DSP is no exception. Digital Signal Processing (DSP) is the backbone of many embedded systems, yet it’s often misunderstood or over-complicated. But it doesn’t have to be, and in a few paragraphs, I’ll show you how to implement an extremely simple but functional low-pass digital filter.
Low-Pass Signal Filtering
When working with embedded systems and reading data from sources prone to noisy measurements (e.g., temperature sensors), it’s common to need a way to reduce high-frequency noise and reveal the slower, meaningful signal underneath. One effective approach is using a low-pass filter, which allows lower frequencies through while reducing higher frequencies. Low-pass filters are especially useful for cleaning up signals from ADCs (Analog-to-Digital Converters).
Now, let’s explore how to implement a digital version of this filtering technique.
Low-Pass IIR Filter
There are multiple types of digital filters available, but we’ll focus on implementing an IIR (Infinite Impulse Response) filter. Without diving too deeply into specifics, these filters incorporate feedback from the output into the input, effectively creating a recursive filter. Such filters are typically less complex, resulting in strong performance that is particularly valuable for embedded systems. It should be noted, however, that the feedback mechanism may impact stability, although we’ll ignore this potential issue in this blog post.
The actual filter calculation is very simple, we have to run this formula from Wikipedia on every input sample to calculate the output: y[i] = α * x[i] + (1 – α) * y[i-1]
Let’s not get confused by all these variables yet, but simplify this formula by rearranging it a bit, primarily to minimize the number of operations to improve performance: y[i] = y[i-1] + α * (x[i] – y[i-1])
We can now explain these variables:
- x[i] is the filter input. For example, a new sample we received from ADC. Remember that we must execute this calculation for each input sample
- y[i] is the filter output (filtered signal)
- y[i-1] is the previous output of the filter. This is the feedback I mentioned above, so the filter output considers the previous output/state of the filter
- a is a magic coefficient that defines the filter – we’ll talk about it in the next section
Calculate Filter Coefficient
The magic coefficient a that I mentioned above determines the filter’s cutoff frequency. This means that signals above this frequency start to attenuate. At the cutoff frequency, the signal is already reduced to about 70% of its input voltage, so it is crucial to choose a cutoff frequency slightly higher than your maximum useful signal frequency.
Besides the desire cutoff frequency, this coefficient also depends on the sample rate, which sounds pretty natural too.
Knowing both the sampling frequency (Fs) and your desired cutoff frequency (fc), we can use an online calculator to calculate this magic coefficient, a.
Filter Implementation (C++)
Once you know the filter formula and the coefficient a, you can implement the filter easily: it’s just one line of code, which you might include, for example, in your ADC interrupt routine:
filter_output = filter_output + a * (new_sample – filter_output);
Note: remember that filter_output variable is also the previous filter state/output, so this variable should persist between calls.
It would also be nice if we could wrap the filter into a simple class and include the logic to calculate the coefficient a, so we don’t have to think about calculating the coefficients online. This implementation is presented below.
Header File
/*
* LowPassIIR.h
*
* A very simple implementation of a basic low-pass IIR filter.
*/
#ifndef INC_LOWPASSIIR_H_
#define INC_LOWPASSIIR_H_
class LowPassIIR
{
public:
// Class constructor, calculates a coefficient based on the parameters:
// sample_frequency and desired cutoff frequency
LowPassIIR(float sample_frequency, float cutoff_frequency);
// Call with method with each sample. It processes the sample and updates the filter
// Returns filtered value
float ProcessSample(float new_sample);
private:
// Calculated a coefficient
float a;
// Filter internal value
float y;
};
#endif /* INC_LOWPASSIIR_H_ */C++ File
/*
* LowPassIIR.cpp
* A very simple implementation of a basic low-pass IIR filter.
* It is based on this article: https://en.wikipedia.org/wiki/Low-pass_filter#Simple_infinite_impulse_response_filter
* It is important to note that the performance of this filter may not be optimal due to C++ and other overheads
* Therefore, for performance-critical applications, it may make more sense to implement the core logic inside the
* ADC interrupt for example
*/
#include <LowPassIIR.h>
// Class constructor, calculates a coefficient based on the parameters:
// sample rate and desired cutoff frequency
LowPassIIR::LowPassIIR(float sample_frequency, float cutoff_frequency)
{
// Calculate a, based on the formula from wikipedia article
// https://en.wikipedia.org/wiki/Low-pass_filter#Simple_infinite_impulse_response_filter
float dt = 1 / sample_frequency;
a = 2 * 3.14159f * dt * cutoff_frequency / (2 * 3.14159f * dt * cutoff_frequency + 1);
// Reset internal sum
y = 0.0f;
}
// Call with method with each sample. It process the sample and updates the filter
// Returns filtered value
float LowPassIIR::ProcessSample(float new_sample)
{
// Update filtered value and return it
y = y + a * (new_sample - y);
return y;
}Will the DSP Filter Slow Down my Embedded Device?
DSP performance is always a concern with signal processing on embedded systems. Although this filter is so basic, it should not affect the performance too much. But let’s test it.
For demonstration, here is how the above class runs the STM32F429 Nucleo board with MCU configured at a modest 50MHz speed.
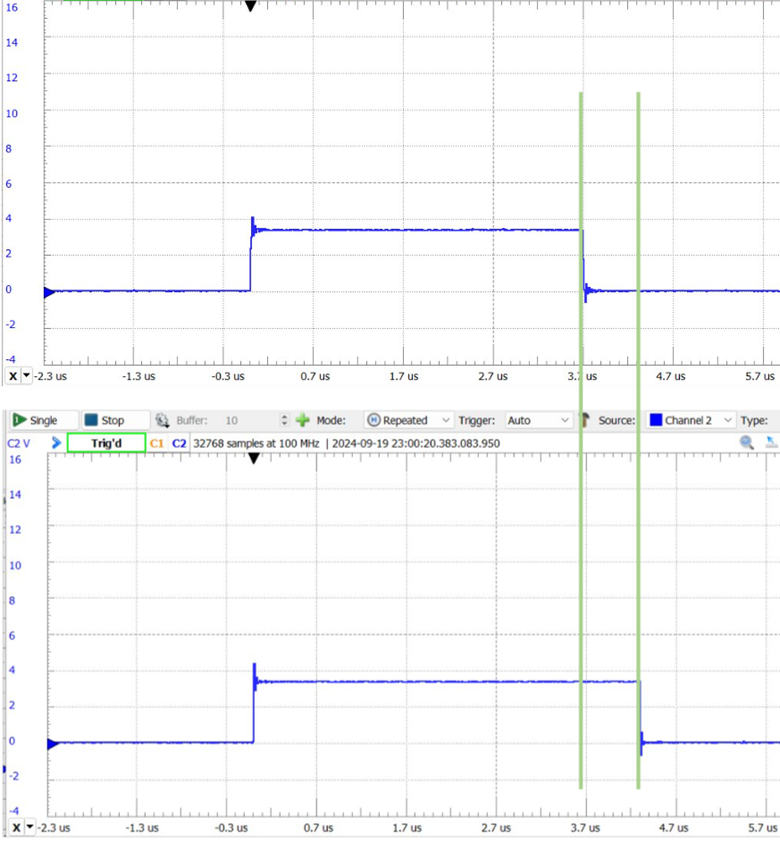
- The first screenshot shows ADC interrupt time, without calling the filter
- The total ADC interrupting handling time is ~3.7us
- The second screenshot is when we are calling the ProcessSample method within the ADC interrupt.
- The total ADC interrupt handling time increased to ~4.3us
- It means that the filter adds 4.3us – 3.7us = 0.6us per sample
This demonstrates that this low-pass filter introduces minimal overhead, making it an excellent choice for embedded systems.
This is a very simple illustration of DSP techniques. If you need support with DSP, whether basic or advanced, please contact us today to learn more about our solutions and how we can help you achieve your goals.







