Three people successfully solved the Equilibrium Angle Geek Challenge. They were Dan Freve of DMC, Brandon Williams of Yaskawa and Jeff Winegar of DMC.
The correct answer is C: a ≈ 50 degrees
The interpretation of this answer is that if the bar is released from the wall at an angle <50°, it will fall back to the wall with the bar still suspended from its bottom point. If the angle is >50°, the angle will increase, the bar will invert and ultimately dangle from its top point.
All three used the principals of statics to solve the problem. Statics tells us that the two conditions for an object to be in equilibrium are that the vector sum of all forces acting upon the object must be zero, and net moment acting on the object must also be zero.
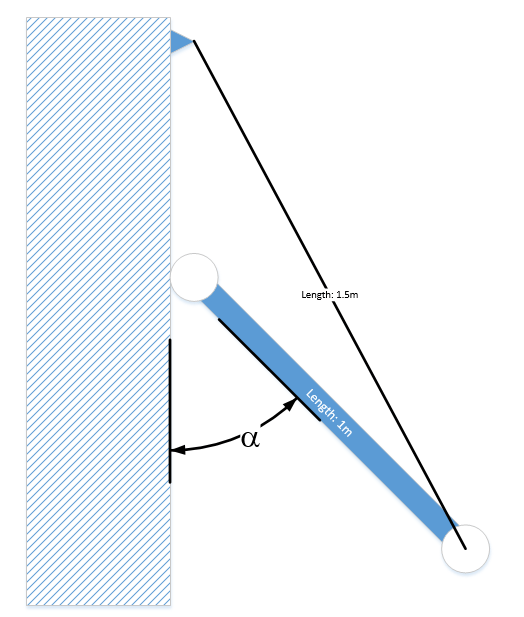
The starting point for a solution by statics is a free body diagram. Jeff Winegar supplied the best one. Here is his free body diagram of the bar:
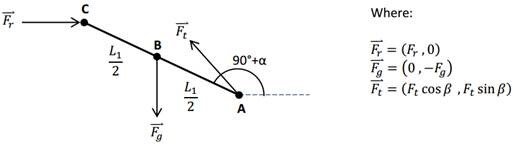
Jeff also gets props for using vector notation and matrices in his solution. However, of the three solutions, only Dan Freve solved the equilibrium angle down to a simplified expression as a functions of the rope length, L. Here is Dan’s solution:
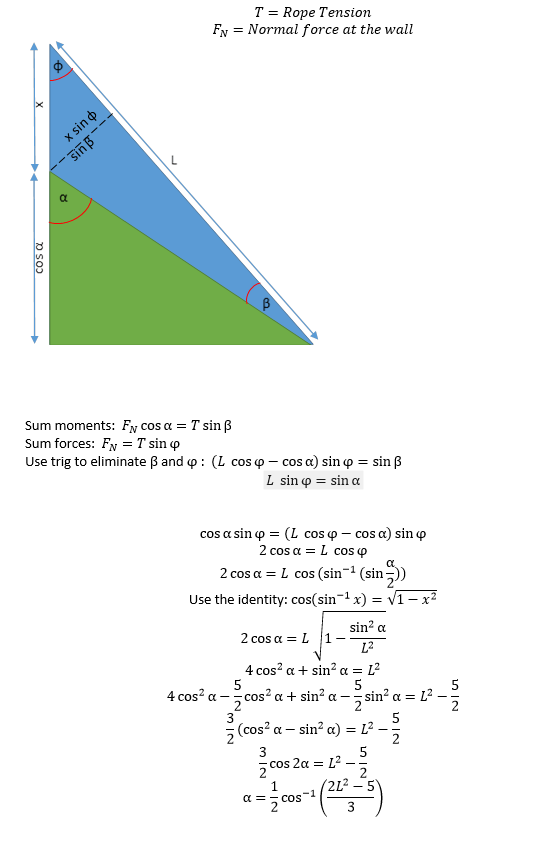
for L = 1.5, α~50 deg (answer C)
A plot of a vs. rope length L, shows that at or above 2.0, there is no non-zero equilibrium angle.
All three correct respondents answered that at length 2, there was no non-zero equilibrium angle.
There is another way to solve the problem other than the use of statics: energy analysis. When gravity causes a stationary system to move, the system’s gravitational potential energy decreases as a result. As a ball accelerates down a slope, what kinetic energy it gains comes from gravitational potential, it loses. If there is no change in gravitational potential with respect to change in position, such as a ball on a level surface, gravity will not cause the ball to move. And if there is a change of gravitational potential, such as on a slope, gravity will cause the ball to accelerate in the direction of decreasing gravitational potential - i.e. downhill. The same rule applies for more complicated mechanical systems. If a system's total gravitational potential changes with respect to a degree of freedom, gravity will push the system in that direction with a force proportional to the slope of that relationship.
In the system described in the problem, all of the movable mass is in the bar/wheel system. And since this system is symmetrical, the center of gravity of the bar is at the center. Gravitational Potential is calculated by the following formula:
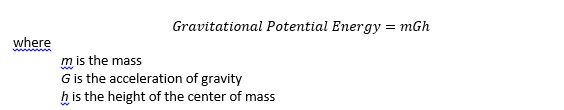
Since m and G are constants, to analyze change in gravitational potential, we only have to concern ourselves with h.
Using some trig, the x position of the lower end of the bar is:
Ax= - sin α
Using the pathagrean theorm, we get the Y position of the lower end of the bar:
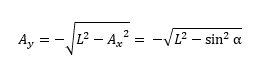
The y position of the center of the bar can be calculated as an offset from the lower end of the bar:
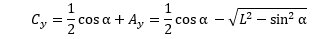
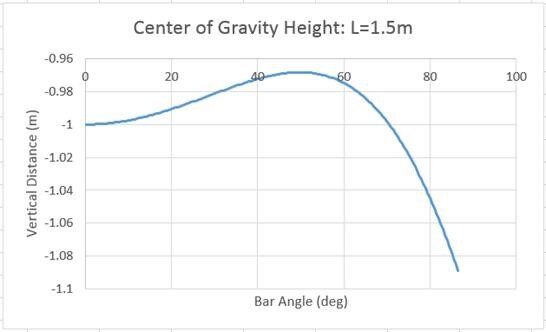
A graph of center of gravity height for L=1.5 plotted with respect to the angle α shows a flat spot around 50 degrees. Since this is the peak of bump, it indicates an unstable equilibrium point from which the system could diverge in either direction.
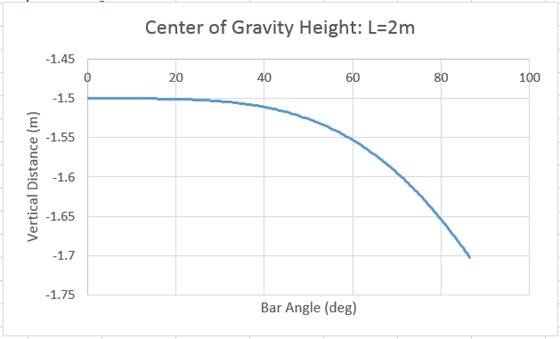
The center of gravity height graph for the 2m rope length is interesting also. It shows no flat spot other than at zero degrees. This corresponds with the mathematical conclusion that the system has no stability point other than at zero. However, it also shows that the flat spot at zero is extremely wide. In fact, the slope stays nearly flat (<0.1% center of gravity movement per bar end movement) for the first 10 degrees from zero. So, in any practical experiment, if the system were constructed with a rope length of 2 meters, the system would also remain stable for any small angle between 0 and 10 degrees.