January's Geek Challenge questioned the construction of a New Year's Eve party beer can pyramid. I first encountered this challenge in my freshman year at Marquette. I was building the beeramid with five other students at a band party, some were engineers and math majors and we couldn't figure it out. I didn't sleep until I found the answer at 4am!
The correct answer for an 8 layer Beeramid is C: 120 cans. Congratulations to this month’s winner, Harry Maddock of the City of Tacoma, WA!
There were eight correct respondents for the Beeramid Geek Challenge. They are:
- Harry Maddock of City of Tacoma, WA
- Dan Freve of DMC
- Gerard Hajduk of Cinch Connectors
- Jason Livermore of Nokia -Siemens Networks
- Jimmy Condon of DMC
- Richard Thiel of Smalley Steel Ring
- Bill Meyer of Wrigley
- Joe Woroby of Nalco
Four people also answered the extra-credit question with 171,700 cans for a 100 layer Beeramid.
All but one person started their solution the same general way:
1 Layer = 1
2 Layers = 1 + (1 + 2)
3 Layers = 1 + (1 + 2) + (1 + 2 + 3)
and so on.
Having established this pattern, the problem was solved algebraically, through programming, and by brute-force counting.
Harry Maddock saw this problem in another way:
One can has been added to all eight levels.
An additional two cans have been added to seven levels.
An additional three cans to six levels.
Etc.
So the total number of cans is (8 * 1) + (7 * 2) + (6 * 3) + (5 * 4) + (4 * 5) + (3 * 6) + (2 * 7) + (1 * 8) = 120
Harry's solution points out another angle of envisioning the problem. Imagine if the pyramid were not made of loose cans, but connected spheres. Also, what if, instead of resting on a triangular base the pyramid (which is now a regular tetrahedron) were balanced on one edge. The lowest layer would be a line of 8 balls. Above that there would be a rectangle of 2x7 balls. Above that would be a rectangle of 3x6 balls. This would go on until reaching the top, which is no longer a point, but a line of 8 balls which is orthogonal to the lowest line. This method also produces Harry's formula of: (8 * 1) + (7 * 2) + (6 * 3) + (5 * 4) + (4 * 5) + (3 * 6) + (2 * 7) + (1 * 8) = 120. Harry wins for his conversion of this very triangular problem into a simple series of rectangles.
Arriving at the Extra Credit result for 100 layers requires either a computer, way too much time, or using algebra to derive a general formula. The algebraic problem was most elegantly expressed by Joe Worobey:
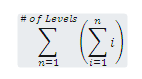
Algebraic Solution:
Dan Freve and Jason Livermore both demonstrated algebraic solutions to this problem. Here is Dan’s:
For each level, t(n), the number of cans in the level is the triangle series is the summation of consecutive integers from 1 to n, which is represented as:
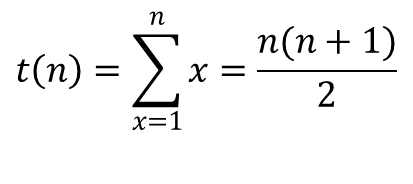
So, the finite sum of the triangle series (I'll call it p(n) for the pyramid) is represented as:
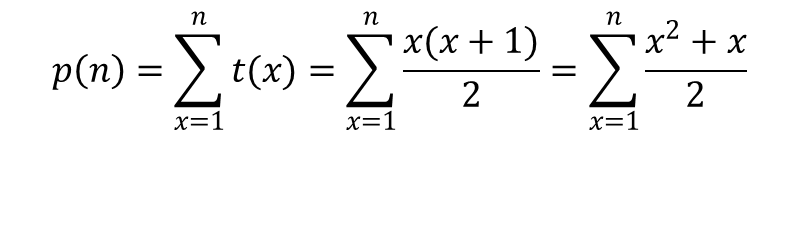
We can simplify this by breaking it into parts:
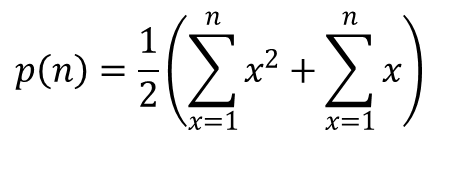
The general form for the second term in this summation is trivial (it’s the same as t(n)). However, I had to look up the general form for the quadratic term:
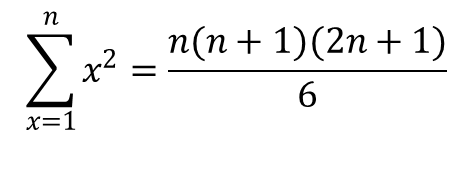
So, now we can substitute into our equation for p(n) and simplify:
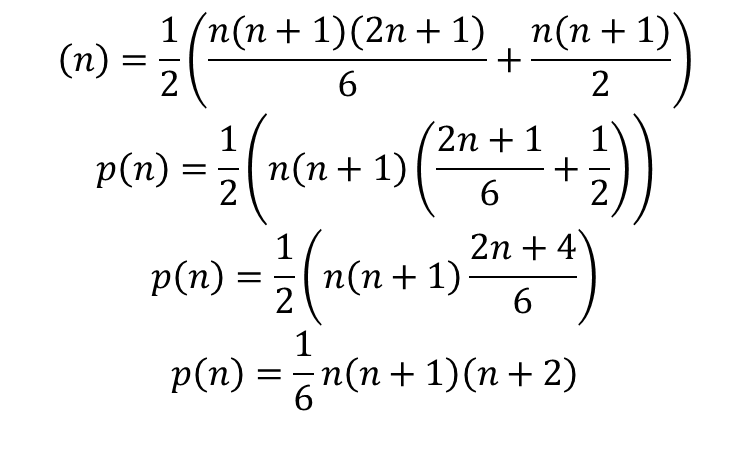
Now that we have the general form, the answers can easily be calculated:
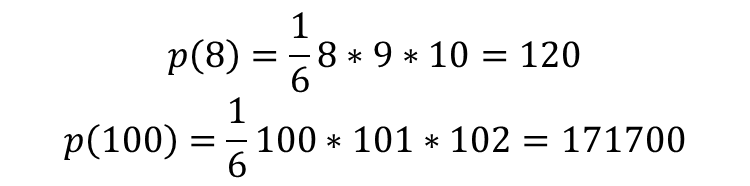
The crux of the algebraic solution is that step in the middle where a polynomial representing 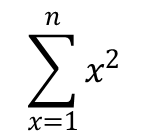 is needed. Nowadays you can just look this up in Wikipedia. When I solved my first Beeramid in 1992, Al Gore was still inventing the internet, and I didn’t know I needed a copy of Fibonacci’s Liber Abaci to see how he solved it in 1202. And I don’t much like inductive proofs anyway because they presuppose that you know or have correctly guessed at the answer. So I came up with my own unique straight-forward solution, which I have now published here.
is needed. Nowadays you can just look this up in Wikipedia. When I solved my first Beeramid in 1992, Al Gore was still inventing the internet, and I didn’t know I needed a copy of Fibonacci’s Liber Abaci to see how he solved it in 1202. And I don’t much like inductive proofs anyway because they presuppose that you know or have correctly guessed at the answer. So I came up with my own unique straight-forward solution, which I have now published here.
Spreadsheet Solution:
For the more practically minded, the full problem can also be solved in about 1 minute using a spreadsheet. Here’s how:
- Fill the first column with the numbers 1 through 100 starting at A1.
- In Cell B1, type the formula: =SUM(A1:A$1)
- Copy cell B1 through to the range B1 to C100.
Having done this, the first column represents the Beeramid height. The second column represents the number of cans in the base level at this height, and the third column represents the total number of cans in the Beeramid at each height. You will see the number 120 in C8, and 171700 in C100.
Submit your comments to: geekchallenge@dmcinfo.com
Learn more about DMC's company culture.