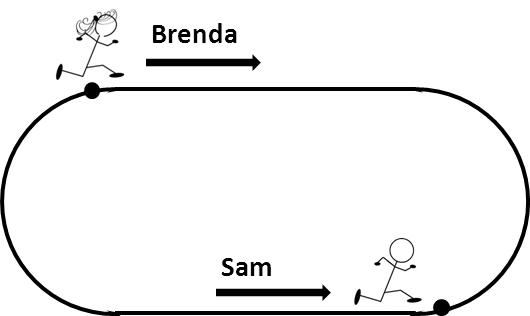
The Sam and Brenda race problem was a fun one to solve. Following simple Distance = Rate * Time methods, it is easy to get to 4 equations and 5 unknowns, which can leave you stuck because the problem doesn’t tell you, and you can never figure out either Sam or Brenda’s speed. However, applying some clever logic to the problem can answer it pretty easily. Here are some additional unstated facts we can conclude from the problem setup:
- When they cross for the first time, they have traveled a total of ½ lap.
- When they cross for the second time, they have traveled a total of 1½ laps.
- When they cross for the third time, they will have traveled a total of 2½ laps
If they traveled at the same speed, symmetry tells us they would always cross each other at the midpoints between their starting points. But if they cross at different positions each time, their speeds must be different. Now, let’s look at the stated figures:
- They first cross each other 100 yards from Sam’s starting point. – This must be 100 yards ahead beyond point in Sam’s direction of motion.
- They cross again as Brenda has 40 yards to go before completing her first lap.
If Sam and Brenda were going the same speed, then the 100 yards from Sam’s starting point would have been the midpoint of a 400 yard track, and the next crossing would be at the other midpoint, 100 yards before Brenda completes her first lap. But that’s not the case. Brenda was only 40 yards from completing her lap when they crossed again, meaning she is running faster than Sam. In fact, between the first crossing and the second crossing, Brenda has gained 60 yards on Sam.
Since their speeds are each constant, and the incremental distance traveled between the second and third crossings is the same, the faster runner should gain the same amount of ground between the second and third crossings as was gained between the first and second. Since Brenda gained 60 yards between the first and second crossings, she will gain an additional 60 yards between the second and third crossings for a total of 120 yards. Since Sam and Brenda first crossed 100 yards ahead of Sam’s starting point, the third crossing will be 120 yards behind that point, or 20 yards behind Sam’s starting point. Thus the answer is A, 20 yards.
The Extra Credit portion of the problem involves finding the circumference of the track from these facts. For that, a fantastic answer was submitted by Jesse Batsche of DMC:
Let C = Circumfrence of Track
Let Vs = Sam’s Speed
Let Vb = Brenda’s Speed
t = Time at first crossing
Since the total distance at the first crossing is ½C, and the total distance at the second crossing is 1½C, then the time at the second crossing is 3t (3= 1½ / ½ ).
Then
(eq. 1) Vb * t = C/2 - 100
(Brenda, at the first crossing, is 100 yards short of half a circumference)
(eq. 2) Vb * (3t) = C – 40
(Brenda at the second crossing is 40 yards short of a full circumference)
Now applying some algebra:
Vb * t = (C – 40) / 3
And substituting equation 1.
C/2 – 100 = (C – 40) / 3
3C – 600 = 2C - 80
C=520