The question posed during last month’s Geek Challenge was to determine how much it costs me in extra gas to drive to my summer road trip destination at a higher speed, and to express this cost measured against the time I save by driving there faster. I provided the following Fuel Mileage chart for reference:
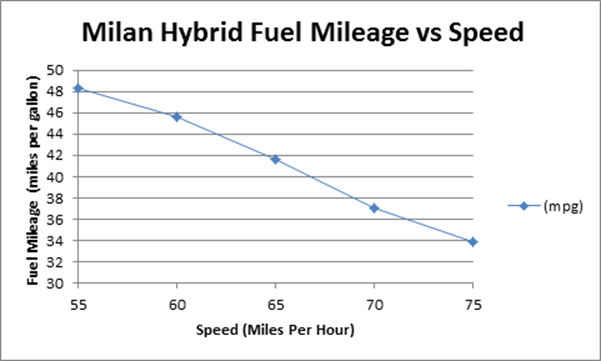
I did not provide the distance to my destination, but that turns out not to matter. Also, because the math on this Geek Challenge is unusually simple, I left it up to each person to pick numbers off of the graph. Let’s say, that my trip was 100 miles. Two scenarios can be calculated:
- Fuel Mileage= 41.7 mpg
- Gallons Burned = 100 miles /41.7 mpg = 2.40 gallons
- Time = 100 miles / 65 mph = 1.54 hours
At 75 MPH:
- Fuel Mileage= 33.8 mpg
- Gallons Burned = 100 miles /33.8 mpg = 2.96 gallons
- Time = 100 miles / 75 mph = 1.33 hours
So the differences between the scenarios are:
- 2.96 gallons – 2.40 gallons = 0.56 extra gallons burned
- 1.54 hours – 1.33 hours = 0.21 hours saved
So the cost rate for driving at 75 instead of 65 MPH is:
- 0.55 gallons / 0.21 hours = 2.71 gallons/hour
- Times $4 per gallon = $10.84 per hour
So the best answer is C, $11 per hour.
This month’s winning answer was submitted by DMC’s John Sullivan. He had another way to make the calculation which went like this:
I calculated ~10.3$/hr. The closest answer is C. with the following equations:
Assume:
34 m/gal @ 75 m/hr
41.5 m/gal @ 65 m/hr
Then:
75 m/hr * 4 $/gal / 34m/gal = 8.82 $/hr
65 m/hr * 4 $/gal / 41.5m/gal = 6.27 $/hr
Solve for X in:
75 m/hr (X hrs) = 65 m/hr (X + 1 hrs)
X = 6.5 hrs
So for every 6.5 hours at 75m/hr, it would take 7.5hrs at 65m/hr
6.5 hr * 8.82 $/hr = $ 57.33 for a 6.5hr trip
7.5 hr * 6.27 $/hr = $ 47.03 for a 7.5hr trip
Therefore for every hour saved in travel time you spend $10.30 more in fuel cost.
John’s method worked perfectly, and would have arrived at the exact answer but for approximations made in interpolating the graph. This method algebraically demonstrates how the length of the trip is irrelevant.
The answer of $10.8 per hour, is specific to my vehicle at moderate temperatures. For a more complete understanding of the additional fuel cost versus time savings associated with driving faster in a wider range of vehicles, we asked one of our customers for some additional data. Mike Duoba at Argonne National Laboratory’s Advanced Powertrain Research Facility provided a report showing steady-state vehicle mileage for several vehicles. I added data from that report to the data I collected from my vehicle’s computer, and plotted it together on this graph:
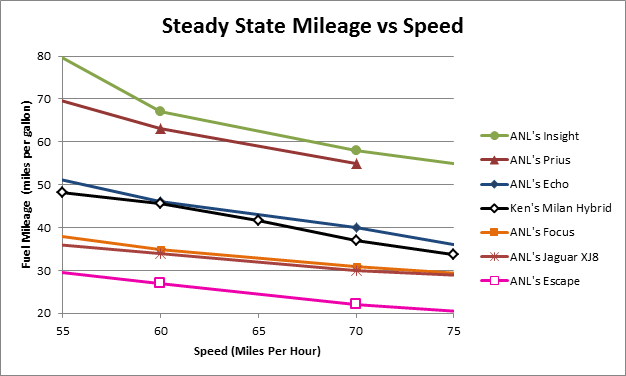
Interpolating the Argonne data, and using the same method for all of these vehicles as I used for my own, I arrived at the following chart of cost of saving time by driving faster calculated between 75 MPH and 65 MPH (assuming $4 per gallon):
ANL's Prius 3.88 $/h*
ANL's Insight 4.25 $/h
ANL's Focus 7.01 $/h
ANL's Echo 8.82 $/h
ANL's Jaguar XJ8 6.30 $/h
Ken's Milan 10.84 $/h
ANL's Escape 15.53 $/h
*Prius value calcualted from 60 MPH to 70 MPH because faster data was not available.
This type of cost/benefit calculation, however, is not dependent having a large range between the speeds compared. For instance, if saving time by driving 75 instead of 65 costs me about $10 per hour in my car, then a very similar rate exists for the decision to drive 62 instead of 61. In fact, for any speed the cost of driving at steady state slightly faster (or amount saved by driving slightly slower) can be calculated as a function of the MPG value at that speed and the slope of the efficiency curve at that speed. The formula for the Cost of Time Saved (CTS) is:
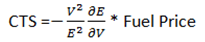
Where:
CTS = Cost of Time Saved (dollars per hour)
V = Velocity (miles per hour)
E = Efficiency (miles per gallon)
Applying this formula to the data I collected for my car yields the following table:
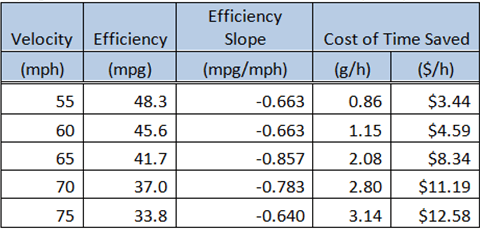
As you can see, the cost of driving faster increases with higher speed. A practical example of how to use this info for an optimization is as follows: If I am driving home and am paying a babysitter $8 per hour while I am gone, I should drive at just under 65 MPH to minimize my total expenditure. If I drive any faster, I pay more in gas than I save by cutting the sitter’s time short. If I drive any slower, I pay the sitter more than I save in gas. This optimization doesn’t assign any value to my own time, which would probably just be spent doing another analysis like this one.