I hope you had a good time hunting for the solution to the Easter Egg Stumper. The challenge was to most efficiently identify one peanut-butter Easter egg from a group of 11 identical chocolate eggs knowing only that the peanut-butter egg weighs differently, and having a traditional balance scale.
Several people answered that it could be done in the worst case in 4 weighs (B), or that 3 could be used if it was known that the peanut butter egg was either heavier or lighter than the others. This method follows and assumes that the peanut butter egg is known to be lighter. (This method from Rob Greve)
1) weigh 6 and 6 eggs, discard the heavier batch
2) weigh 3 and 3 eggs, discard the heavier batch
3) now weigh 2 eggs, if they are the same, the third is your peanut butter egg. If one is lighter, that is your peanut butter egg.
However, a method exists to determine the peanut-butter egg without knowing whether it is lighter or heaver to begin with. In fact, this method also results in that answer after 3 weighings (A). This method was uncovered by Dan Freve of DMC and Paul Benjamin of Rockwell Collins.
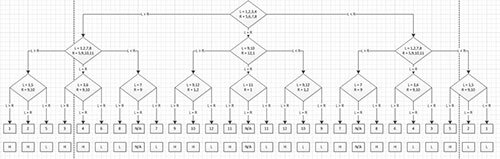
You can use the scale to do a “trinary” search since you can split the eggs into three groups each weighing (left side, right side, and off the scale). Weigh as follows:
1. Split the eggs into 3 groups of 4 and weigh the first 2 groups – worst case is the scale is not balanced and you only learn which 8 eggs the PB egg is among
2. Split the 8 eggs into three groups (3, 3, and 2). One group stays in its original tray, the 2nd group switches to the opposite tray, and the third group gets removed from the scale. If the scale tips the same direction, the PB egg is in the group that stayed. If it tips in the opposite direction, the PB egg is in the group that moved. If the scale balances, the PB egg is in the group that was removed from the scale.
3. Repeat this for the 3rd weighing and you’ll have the answer. The cool part about this method is that you’ll also know if the PB is heavier or lighter by the time you’re done with the 3rd weighing.
And for clarity, here decision chart to take you through the process (click for full sized image).
Paul Benjamin recognized this Geek Challenge as a cleverly disguised version of the 12 Weighings Problem, and that the answer was available online. Here are some links which describe its solution, and some variations which include optimum methods for finding the odd weight in an arbitrarily sized sample:
http://www.iwriteiam.nl/Ha12coins.html
http://en.wikipedia.org/wiki/Balance_puzzle