Last month, we asked you to find the odds that a class of 23 students has one or more shared birthdays. The correct answer to the Baffling Birthdays question is C: 50.7%.
The winner of this month’s Geek Challenge is John Jacobsma of Dickson. His answer covered the basics, as well commented on the problem’s implicit assumptions.
There were several people who also correctly answered this month’s Geek Challenge. They are:
Jesse Batche of DMC
Joseph C. Bond
Matt McNamara of Dickson
Robert Salm
Sam Weber of DMC
First, John called the author out on using asking the wrong question: what are the odds, as opposed to what is the probability.
Next, there’s the matter of whether a random group’s birthdays are evenly distributed among the possible dates, and whether February 29 is one of those possible dates. Since the group in question is first graders, and it is currently fall of 2013, those born on February 29, 2008 are 5½ years old. They have substantially missed the common September 1 deadline to turn 6 and enter first grade. So, there are 365.0 possible birthdays.
The next issue is whether birthdays are evenly distributed. It turns out that they are not, but for purposes of this challenge, I think they are close enough. I found a discussion of this here. The source of this data is 480,000 policy applications to a life insurance company.
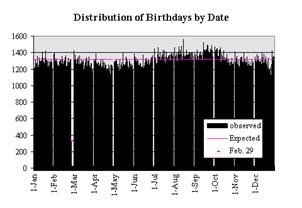
Getting back to the question, the way to compute the probability of a group having at least one duplicate birthday is to calculate the probability of it not happening, and subtract this probability from 1. The null-case for having a duplicate birthday is that all students’ birthdays are unique among the group.
So, with one person in the group, there is a perfect chance, or 356/365 that that birthday is unique. The second person has a 364/365 probability of a unique birthday, or not duplicating the first person’s. The third person has to avoid two birthdays, so that probability of being unique is 363/365, and so on.
Therefore, the calculation for 23 students to have unique birthdays is: (365*364*363*...*345*344*343) / (365 ^ 23) = 0.4927
The probability of a duplicate birthday is 1 - 0.4927 = 0.5063 or 50.7%
Here is John’s full answer:
The answer, of course, is none of the above, because the question asks for the "odds", and the supplied answers are all given as probabilities expressed as percentages. Odds are a ratio between the chance of an event occurring and it not occurring. For example, if I flip a "fair coin", there is a 50% chance it will come up tails, but the odds of it coming up tails are 1 to 1 (even odds). So converting the answers to odds, the choices are: A. 16.2 to 1 against B. 1 to 1 C. 1.03 to 1 for D. 3 to 1 for
Now the answer becomes "not enough information given."
In order to solve the problem, we need to make some assumptions. Specifically, we need to assume the students' birthdays are uniformly distributed over the range of days in a year, and independent of one another. Also, we need to know whether the year from which the first grade population is drawn included a February 29 or not, as duplicate birthdays will be slightly less probable in a 366 day year, as opposed to a 365 day year.
The assumption that birthdays are uniformly distributed is most likely untrue, but it is a reasonable assumption, because the variance from uniform is likely to be small enough that the effect on the probability of duplicates will be negligible.
However, given the possibility of multiple births, the assumption that the birthdays are independent events is not reasonable. Since the population is first graders in a single school district, siblings of the same age would attend the same grade in the same school. So, to answer the question properly, we would need to know the school's policy on whether to keep siblings together or split them up into different classes.
A little internet research tells us that the frequency of multiple births in the US is currently about 3.3%. So, if the school policy is to keep siblings together, the probability of a class of 23 students having no twins (or triplets, etc.) would be
(1 - 0.033) ^ 22 = 0.477950
The exponent is 22 instead of 23 because a member of a multiple birth would not be chosen as the last member of the class.
Given a class of 23 with no multiple births, the probability of no multiple birthdays is then
(365*364*363*...*345*344*343) / (365 ^ 23) = 0.492703
We're assuming the students were born in a 365 day year, not a leap year.
Therefore, the probability of no multiples births and no duplicate birthdays is
0.477950 * 0.492703 = 0.235487
Which makes the chance of having duplicate birthdays
(1 - 0.235487) = 0.764512
Which makes the odds of having duplicate birthdays
764512 to 235487 for having 1 or more duplicates in the class of 23
or
3.24651 to 1, which can be rounded to 13 to 4 for having duplicates
Of the answers given, D (75%) is the closest, unless the school policy is to separate siblings, in which case C (50.7%) is the correct answer. Unless the school is in Nigeria, where the rate of multiple births is the highest in the world, 1 in 22 (4.5%). (I leave calculating the exact odds for a Nigerian school as an exercise for the reader.)
Whether siblings are separated or not, having duplicate birthdays in 4 of the 8 classes is not improbable enough to be considered anomalous.
Submit your comments to geekchallenge@dmcinfo.com.
Learn more about DMC's company culture.