A number of points (N) are distributed along the circumference of a circle. Every point is connected to every other point by a chord. The points are spaced unevenly such that no more than two chords intersect at a common point inside the circle.
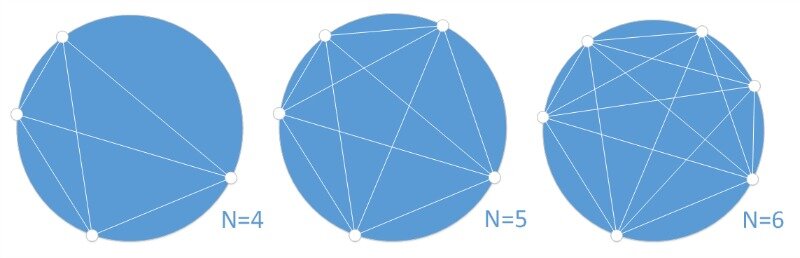
As demonstrated in these figures, when there are 4, 5 and 6 perimeter points, there are 1, 5 and 15 internal chord intersections respectively.
If N=8 (circle with 8 points on the perimeter), how many internal cord intersections are there?
A: 56
B: 64
C: 70
D: 85
Extra Credit: Produce a simplified expression that represents the number of internal chord intersections as a function of the number of perimeter points (N).
As always, the answer with the best analytical content will be this month’s Geek Challenge winner!
Submit your responses to geekchallenge@dmcinfo.com.
Comments
There are currently no comments, be the first to post one.