Thirteen people correctly answered the Crossing of the Chords Geek Challenge by selecting C: 70 intersections. In their explanations, two very distinct methods were demonstrated to arrive at the general equation for intersections as a function of perimeter points. This month’s winners are John Jacobsma of Dickson, Devon Fritz of DMC, Sudeep Gowrishankar of DMC, and Adnaan Velji of DMC. They used a Combinations method to arrive at the method very efficiently.
To give proper context to the extreme efficiency of the Combinations solution to this problem, I will first demonstrate the more common Series method. Actually, I’ll let Andrea Gotti of Ingersoll explain:
N : number of points unevenly distributed on the circumference. No more than two chords intersect at a common point inside the circle.
I : number of internal chords intersections. Starting from the images above one can observe as follows:
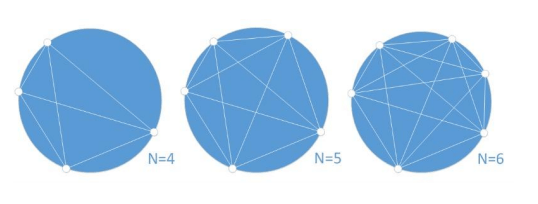
These numbers can be conveniently collected by using the following table:
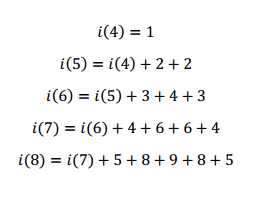
The index is used just to keep a compact notation. The number of intersections, expressed as a function, is the sum of all the elements in the first rows.

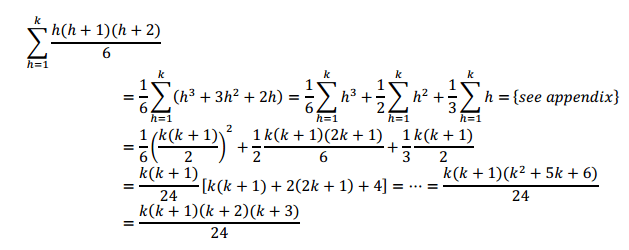
Therefore, the original problem has become:
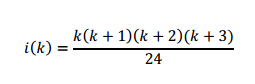
The formula can now be expressed as a function of N:
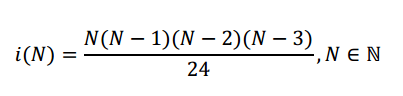
So, substituting to arrive at the final answer:
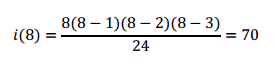
Wow, that’s a ton of work, and is what the majority of people who answered this question actually went through. A few people, however, found an easier way. Here is a winning solution from Devon Fritz:
Every set of four perimeter points produces an intersection point between that set of four points.

So, for each set of unique 4 points on the perimeter, a unique intersection point is formed. This can be written mathematically as a combination formula for N>3: NC4
The formula for combinations can be expressed with factorial:
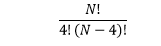
And substituting the required perimeter points:
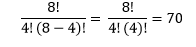
OBSERVATION #1: By moving from one row to the next one below, the number in the first column increases by 1, the one in the second by 2, the one in the third by 3, and so on. This allows one to state the problem by using the following recursive formula:
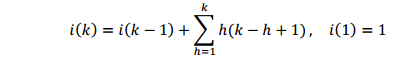
For example:
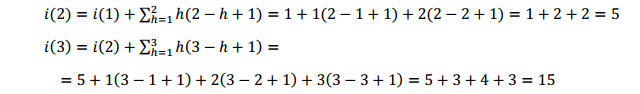
Consider the term: 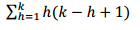
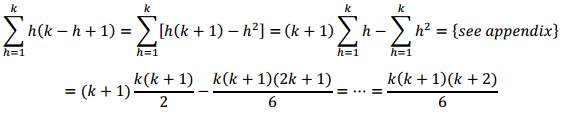
The original problem can now be expressed via this simplified recursive formula:
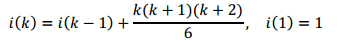
For example:
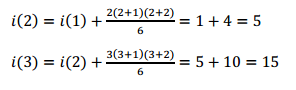
OBSERVATION #2:
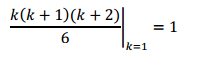
This allows one to reformulate the problem as follows:
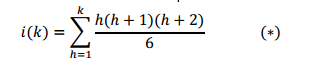
Let's now consider the term: 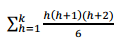
And thus, our winners were selected for representing the results of three jam-packed pages of math with just 3 letters: NC4
So, congratulations again to John Jacobsma, Devon Fritz, Sudeep Gowrishankar and Adnaan Velji for winning this Geek Challenge!
Submit your comments to geekchallenge@dmcinfo.com.