The results are in! Two people correctly answered December's geek challenge.
Ken Brey of DMC and Jesse Batsche of DMC both identified the correct percentage as D: 60-65%. Ken supplied an exact solution for the probability as the grid of pool balls becomes infinitely large.
However, Jesse is this month's winner because he wrote a really cool LabVIEW program to solve the problem!
Ken's Exact Solution
Where X and Y represent the row and column offset of a ball relative to the cue ball, given 4-way symmetry, we can analyze only 1/4 of the space, such that X>0 and Y>0. Now we can use only natural numbers. Given an infinitely large surface, the probability of selecting a ball on the symmetry lines of X=0 or Y=0, rows is infinitely small, and therefore ignoring these can’t affect the outcome.
For a ball at X,Y to be a clear shot, there must be no smaller similar right triangle with integral sides to the right triangle with sides X and Y. So, for all n smaller than X and Y, X/n and Y/n must not both be integers.
In other words, X and Y are coprime, or the greatest common divisor (GCD) of X and Y is 1. A simple solution for the probability of this question of the probability of GCD being 1 for an infinite set of integers was figured out by a couple of bright undergrads in 1992. Their answer matches more complicated proofs discovered earlier. The answer is 6/pi² or 60.7927%.
References:
http://www.cut-the-knot.org/m/Probability/TwoCoprime.shtml
Aaron D. Abrams and Matteo J. Paris
The College Mathematics Journal
Vol. 23, No. 1 (Jan., 1992), p. 47
Jesse's LabVIEW Solution
Jesse correctly approximated the percentage by building a LabVIEW program to solve the problem for arbitrarily large grids of pool balls. Jesse's solver iteratively "takes shots" at balls in "rings of increasing radius" (i.e. starting with balls closest to the cue ball, moving outward). It keeps track of shot angles that it has already taken to hit a prior ball. If it aims at a ball, and it requires exactly the same shot angle as a previous ball, then that ball is deemed un-hittable. In addition to calculating the ratio for any size grid Jesse's solver includes an awesome animated graph showing the hittable and unhittable balls in the grid as it iterates through them. Green boxes represent hittable balls and boxes left red represent unhittable balls.
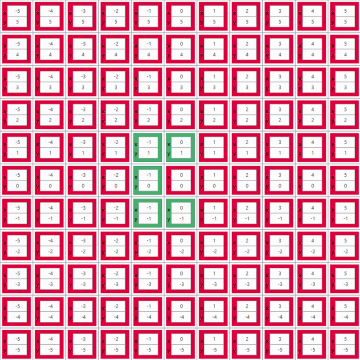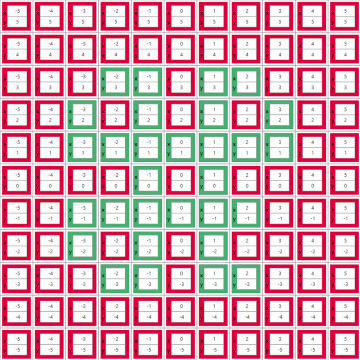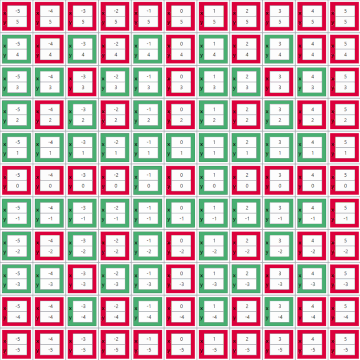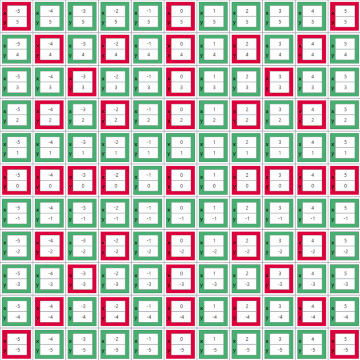
The results are then shown in a more condensed grid. Shown below are the results for a 103x103 grid.

Congrats to our winner, Jesse, who receives a retro logo DMC pocket protector!

Submit your comments to geekchallenge@dmcinfo.com.
Check out all the past challenges here!