The results are in! February's Geek Challenge winner is Grant Anderson of DMC. Grant's clever breakdown of the problem is shown below.
Grant's Solution
There are five classifications of locations that satisfy this riddle (at least on the surface):
- As mentioned in the riddle itself, the North Pole.
- All locations one-mile north of the one-mile long parallel of latitude in the Northern Hemisphere.
- All locations one-mile north of the one-mile long parallel of latitude in the Southern Hemisphere.
- All locations one-mile north of a parallel of latitude which is an integral fraction of a one-mile long parallel of latitude in the Northern Hemisphere.
- All locations one-mile north of a parallel of latitude which is an integral fraction of a one-mile long parallel of latitude in the Southern Hemisphere.
For ease of calculations, we’ll assume the earth is perfectly spherical, rather than the ellipsoid it truly is. Also, since this isn’t a geography question, we’ll assume that our traveler won’t have to take elevations into consideration and place him at sea-level for his entire trip.
There are 90 degrees of latitude between the equator and each pole (the equator being 0 degrees). The circumference of the Earth at the equator is 24,901.92 miles, which, dividing by 360 degrees, means that each degree of longitude at the equator is 69.172 miles.
However, because we are assuming a perfectly spherical earth, we know that each degree of latitude on the Earth is also 69.172 miles. As our traveler moves closer to the poles and away from the equator, the mileage difference between each degree of longitude shrinks.
We’ll first solve for the two parallels of latitude where 360 degrees of longitude is exactly one mile. Or alternately, 1 degree of longitude is 0.0028 miles.
To calculate at which degree of latitude 1 degree of longitude is equal to 0.0028 miles, we can use the following calculation:
1 degree of longitude = cosine (latitude in degrees) * mile length of a degree at the equator
So, plugging in our values we have:
0.0028 = cosine(x) * 69.172
Solving for x gives us:
x = 89.998 degrees
Northern Hemisphere
In the Northern Hemisphere, our traveler needs to go one mile north of 89.998 degrees. Since we know each degree of latitude is 69.172 miles, we find the traveler will need to start out at the 89.998 + (1 / 69.172) degrees North latitude or 90.012 degrees North latitude.
This means he is actually crossing through the North Pole. The upshot is, we can scratch classifications 2 and 4 from the list above. It’s impossible to do this from the Northern hemisphere other than at the North Pole, assuming that you can’t actually walk north of the North Pole.
Southern Hemisphere
In the Southern Hemisphere, once again the traveler needs to go one-mile north of 89.998 degrees, which puts him at 89.983 degrees. One degree of longitude here equals cosine (89.983) * 69.172 or 0.0205 miles. Multiplying by 360 gives us the length of this latitude as 7.389 miles.
Now, we need to calculate the remaining locations that fall under classification 5, all locations one-mile north of a parallel of latitude which is an integral fraction of a one-mile long parallel of latitude in the Southern Hemisphere.
We now calculate the degree of latitude where 720 degrees of longitude is equal to 1 mile. Using our equation from above we find this is the 89.999-degree south parallel. One mile north of that gives us the 89.984-degree south parallel. And its length is 6.953 miles
Next, we calculate the degree of latitude where 1080 degrees of longitude is equal to 1 mile. This puts our traveler less than a thousandth of a degree south of what we just calculated. At this point, we can assume the width of his hovercar from the previous locations trip will cover this location and all subsequent locations that fit the harmonic series.
So if our traveler starts at the North Pole, he’ll move straight down to the 89.983-degree parallel and circle it. After this, he’ll travel to the 89.984-degree parallel and circle it as well. This trip yields a total distance of:
((90 degrees + 89.984 degrees) * 69.172 miles/degree) + 7.389 miles + 6.953 miles = 12,464.195 miles
Traveling at 100 mph means his trip will take about 125 hours. At over 5 days of travel, he’s going to need those energy drinks.
Additional Thoughts
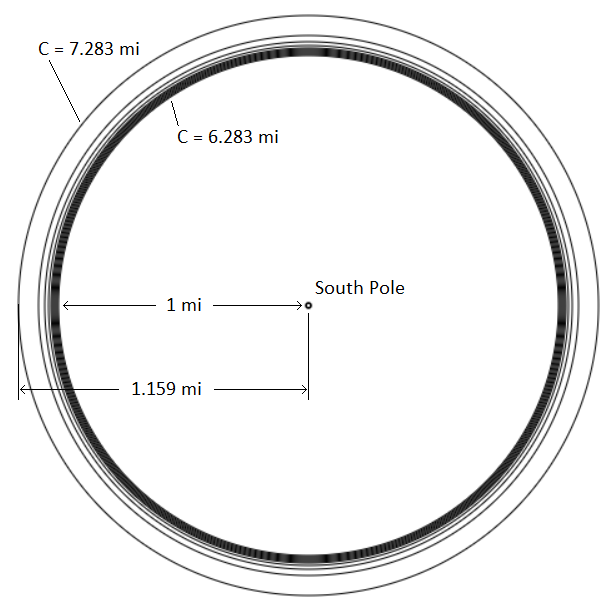
As Grant pointed out, there are an infinite number of rings near the South Pole made from the points that satisfy this riddle. It would be impossible for our traveler to travel along all of these rings since all have a circumference of at least ~6.28 miles (the circumference of the latitude line 1 mile north of the South Pole). This would make our traveler truly eccentric as he would forever travel around the South Pole without ever reaching it (reaching the South Pole would make him a centric traveler).
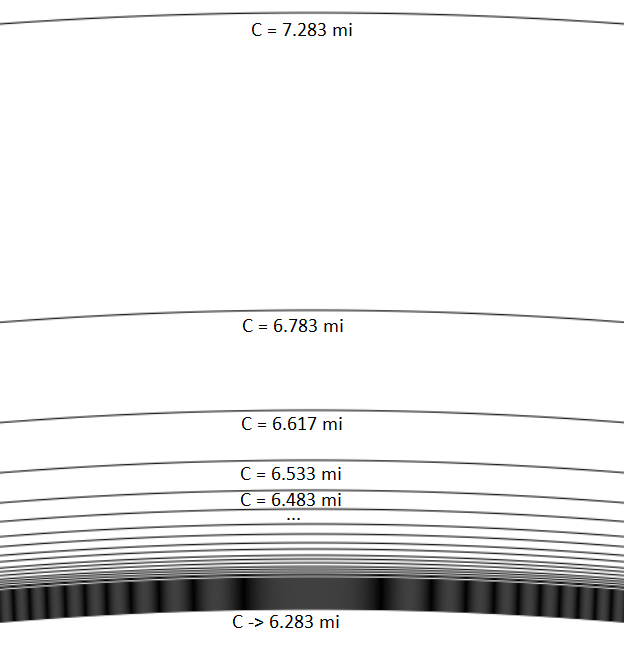
Grant gave our traveler some closure by pointing out that eventually, the rings become so close to each other that the width of his hover car covers multiple rings and at some point spans all remaining rings to be traveled around. To examine this, and see how wide his hover car would need to be, let's take a closer look at his path along these rings near the South Pole. Let's zoom in and see how far apart the rings are.
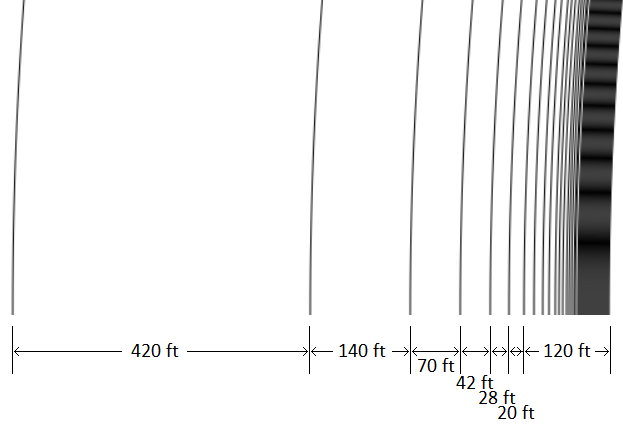
Looking at these distances, we see that if our traveler's hovercar is at least 841 ft wide, he could sweep through all the rings in one loop around. If his hover car is at least 420 ft wide, he could do it in 2 loops, covering the first and second ring in his first loop and all the rest in his next loop.
If his hover car is just the width of a normal car, we see that he'll have to do many loops around before he can cover all of these rings. However, any distance added traveling around these loops is pretty insignificant compared to the first 12,450 miles he travels from the North Pole to the first ring.
One more interesting thing about the spacing of these rings is that the infinite number of points satisfying this riddle, excluding the North Pole, are contained in a relatively small area on the surface of the globe (they are all between 1 and 1.159 miles away from the South Pole).
This area can be calculated as the following surface integral:
\(A = \int_0^{2\pi} \int_{\frac{1mi}{3959mi}}^{\frac{1.159mi}{3959mi}}(3959mi)^2cos(\theta)d\theta d\phi \approx1.076mi^2 \approx689acres\)
3959 mi = Earth's radius
1 mi = distance of inner-most ring from the South Pole (more correctly, what the ring sizes are approaching as they get smaller)
1.159 mi = distance of outer-most ring from the South Pole
The Earth's surface (both land and water) is approximately 126 billion acres, so the area these points are contained in is only 0.0000005% of the total area on Earth!
Submit your comments to geekchallenge@dmcinfo.com.