This content was originally published by Eric Anderson as a white paper.
Overview
This blog describes a procedure for translating a state transition diagram or sequential function chart into a ladder diagram. Ladder diagrams are available on almost all programmable logic controllers (PLC) but writing large programs with complex state-based behavior in ladder diagrams is cumbersome. Instead, the program can be designed with a state transition diagram or sequential function chart and then, if a direct method of programming these structures into the PLC is not available, translated into a ladder diagram. This technique is of particular interested to DMC because many projects we encounter require older or limited hardware platforms.
Table of Contents
Review of Ladder Diagrams and Sequential Fuction Charts
Ladder diagrams are an industrial programming language typically used on programmable logic controllers (PLC). This graphical language mimics a relay logic electrical schematic familiar to electrical technicians. For engineers that are not familiar with relay logic, though, ladder diagrams can be difficult to implement, debug, and maintain, especially when programming complicated machines with state-based behavior. In these applications, the state transition diagram or sequential function chart are better programming tools.
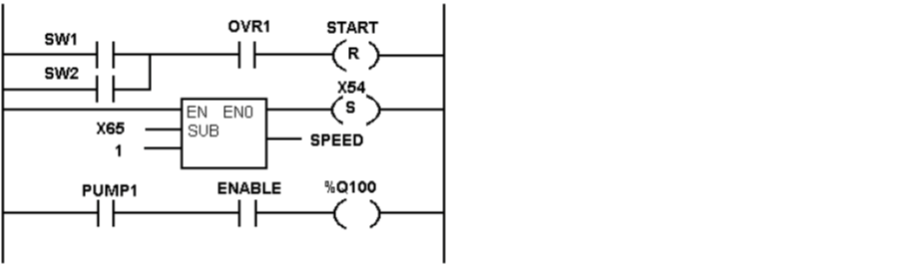
Figure 1: Example ladder diagram (http://www.amci.com/tutorials/tutorials-what-is-programmable-logic-controller.asp, downloaded 8/31/2009)
Both ladder diagrams and sequential function charts are included among five languages standardized in IEC61131-3 for industrial programming (the others being structured text (ST), instruction list (IL), and function block diagram (FBD)). These languages are supported and extended by the international not-for-profit organization PLCopen. But, not all five languages are supported on all PLCs, especially older models, such as the Allen Bradley SLC-500, and inexpensive PLCs, such as those from AutomationDirect. Almost all PLCs, however, support ladder diagrams.

Figure 2: Example Sequential Function Chart (standard_presentation_june2005.ppt from www.plcopen.org, downloaded 8/26/2009)
To use a sequential function chart on a PLC that only supports ladder diagrams, a technique was developed to convert the former to the latter. I was introduced to this technique by Professor Robert D. Lorenz while at the University of Wisconsin-Madison College of Engineering. I've used it on two projects since joining DMC. The first was a software rewrite for a part coating line. The other was a testing machine.
A Generic State
A generic state is pictured below. State A becomes the active state when states B, C, and D are active and the logic to transition to state A (Logic B-A, Logic C-A, and Logic D-A) is satisfied. For example, if state C is active and Logic C-A is satisfied, state C will be deactivated and state A will be activated. State A will be deactivated when the logic to transition away from state A (Logic A-E, Logic A-F, and Logic A-G) is satisfied. Any number of states could transition to or away from state A (more than shown).
The transition logic can consist of physical inputs, the status of timers or counters, or states of other sequential function charts running in parallel with this sequential function chart. Care must be taken to define the transition logic so only a single transition from a state will be satisfied at a particular instant. In the diagram below, this requires that Logic A-E, Logic A-F, and Logic A-G be distinct so which state will become activated (E, F, or G) is not ambiguous. One danger is that more than one state would be activated when state A was deactivated. Some implementations give precedence to the left-most satisfied transition logic. The translation procedure described in this blog does not provide a precedence structure.
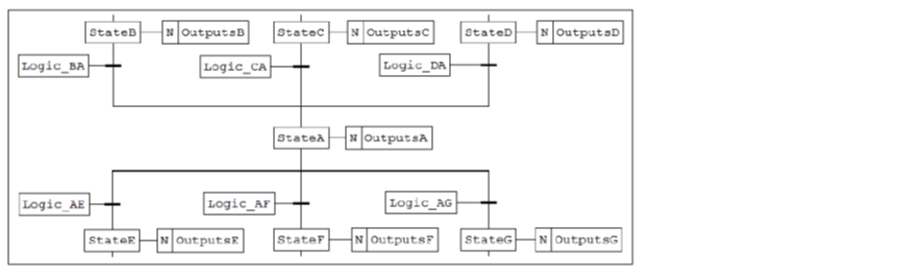
Figure 3: Sequential Function Chart diagram of a generic state
Translation Using Diagrams Primitives
Ladder diagram primitives include the elements listed below. These are core elements based on the relay logic from which ladder diagrams are derived. These should always be available for creating ladder diagrams and may be the most efficient elements in terms of memory usage and execution speed. Ladder diagrams elements not considered primitives are discussed in the next section.

Table 1: Ladder diagram primitives
The ladder diagram rung shown below shows the translation of the generic state described above using ladder diagram primitives. Each state would be translated into a rung structured similar to this one. Whether the state is active or not is represented by the normal output (blue). States preceding the generic state are represented by normally open contacts (red) and states following the generic state are represented by normally closed contacts (orange).
A state is activated when a preceding state is active and the logic to transition to the generic state is satisfied (and a following state is also not active). The generic state is held active by the normally open contact connected to the generic state output (purple). The generic state is deactivated when a state that follows it becomes active. A first-pass system bit is required to set the active state of the machine at start-up.
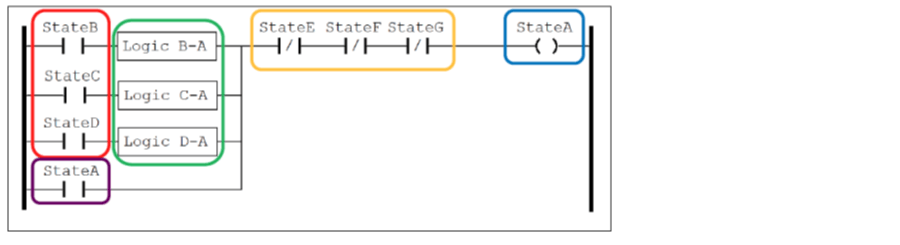
Figure 4: Ladder diagram primitive translation of a generic state using primitives
Outputs are a function of which state is currently active (and states only, making this a Moore-type state machine). The diagram below shows the rung structure for outputs, which would be placed below all rungs that represent states. In the diagram below, Output1 is active in states A and B and no other states and Output2 is active in states A and E and no other states.

Figure 5: Output rungs for the primitive translation of a generic state
Disadvantages of Using Primitives
As mentioned above, primitive ladder logic elements are the most widely available elements and are probably the most efficient in terms of execution. Though the structure of each state rung is relatively simple and straightforward, the rungs must be structured correctly to ensure proper execution order. This results from the fact that ladder diagram execution is performed top-bottom and left-right. If, for example, the rung that activates state E follows the rung that activates state A, state A will not be deactivated until the next scan of the ladder diagram. Having both states active may cause an unsafe mode of operation. This can be handled by introducing a dummy state between states A and E. The outputs shared by states A and E would be activated in the dummy state but other outputs would be deactivated.
A dummy state must also be placed between states that follow and precede each other. For example, if state B also followed state A, state B would appear in the section of normally closed contacts (circled in orange in Figure 4) in addition to the section of normally open contacts (circled in red). This would be the logical equivalent of state A being activated when state B is both active and not active and that is impossible.
These disadvantages reduce the straight-forwardness of the sequential function chart to ladder diagram translation, the ability to debug execution, and maintain the program. These losses outweigh the advantages of widespread support and execution efficiency.
Translation Using Higher Level Operations
Higher level operations refer to those ladder diagram elements that perform more sophisticated operations than merely the setting and getting of bits as performed by the primitive elements. Most PLCs support many higher level operations. The ones used for this translation technique are listed below. The Move block sets the variable connected to OUT equal to the variable connected to IN when the EN input is true. The equality evaluates the inputs IN1 and IN2 when the EN input is true. If they are equal, OUT is set to true.
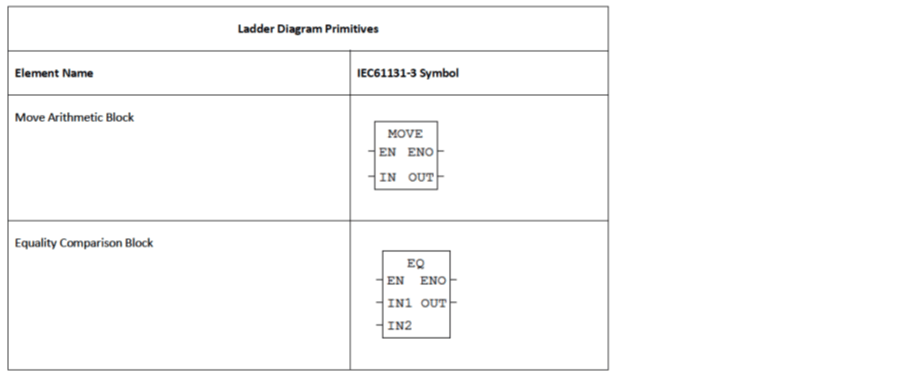
Table 2: Higher level ladder diagram blocks
The ladder diagram rung shown below shows the translation of the generic state described above using higher level ladder diagram operations. A CurrentState variable represents the active state for the current evaluation of the ladder diagram and a PreviousState variable represents the active state of the previous evaluation. Integer constants represent each state. The constant for the generic state is assigned to CurrentState by the move operation (blue). This occurs when PreviousState is a preceding state (evaluated with the equality comparison blocks; red) and the logic to transition to the generic state is satisfied (green).
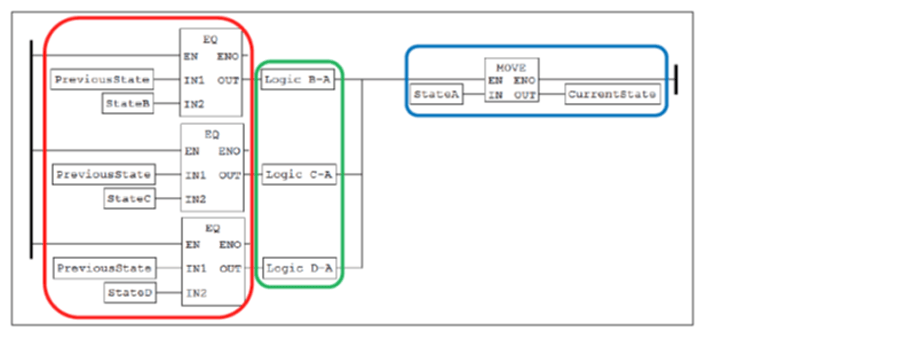
Figure 6: Ladder diagram translation of a generic state using higher-level function blocks
Once all states in the entire sequential function chart are evaluated, PreviousState is set to the value of CurrentState. The generic state is deactivated by setting CurrentState to a value other than the constant for the generic state. A first-pass system bit is required to set the initial values of CurrentState and PreviousState at startup. The PreviousState variable is used to ensure that each state is active for at least one execution of the diagram and not immediately deactivated by a rung below its rung. This, among other things, prevents different behavior due to the order of the rungs.

Figure 7: Updating the PreviousState variable after setting CurrentState
Then, as before, the outputs are evaluated as a function of the states and states only.
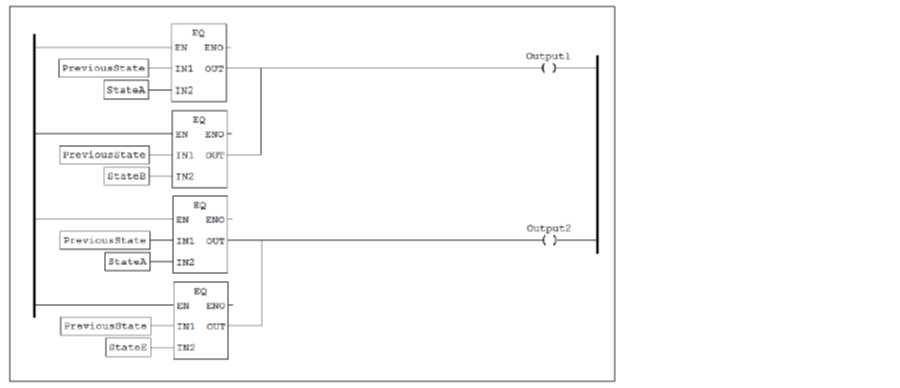
Figure 8: Output rungs for the higher-level function block translation of a generic state
Employing higher level operations makes translation of the sequential function chart more general and straightforward. Due to the use of function blocks, however, execution time may suffer
Simple Example
Below is the sequential function chart and translated ladder diagram for a simple device that toggles a lamp on the falling edge of an input (similar to an old-fashioned flashlight). The N-type actions used to turn the lamp on represent non-stored actions that are only active while the state is active. To turn the lamp on, the input must be turned on and then off. To turn the lamp back off, the input must be turned on and turned off again. The lamp does not turn off until the input is turned off. This simple example is difficult to implement in a ladder diagram without the structured approach outlined in this blog (it would be instructive to try).
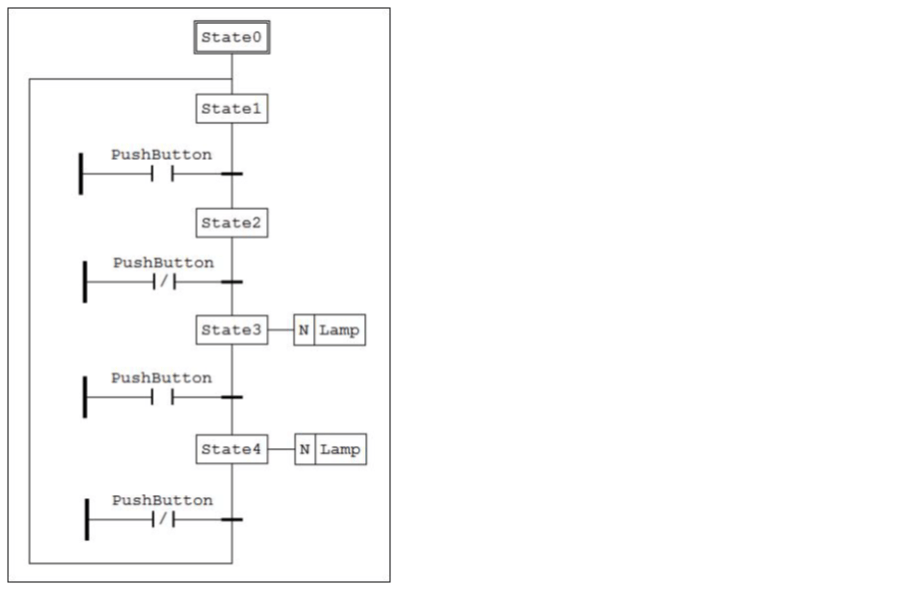
Figure 9: Sequential function chart of a simple toggle-on/toggle-off device
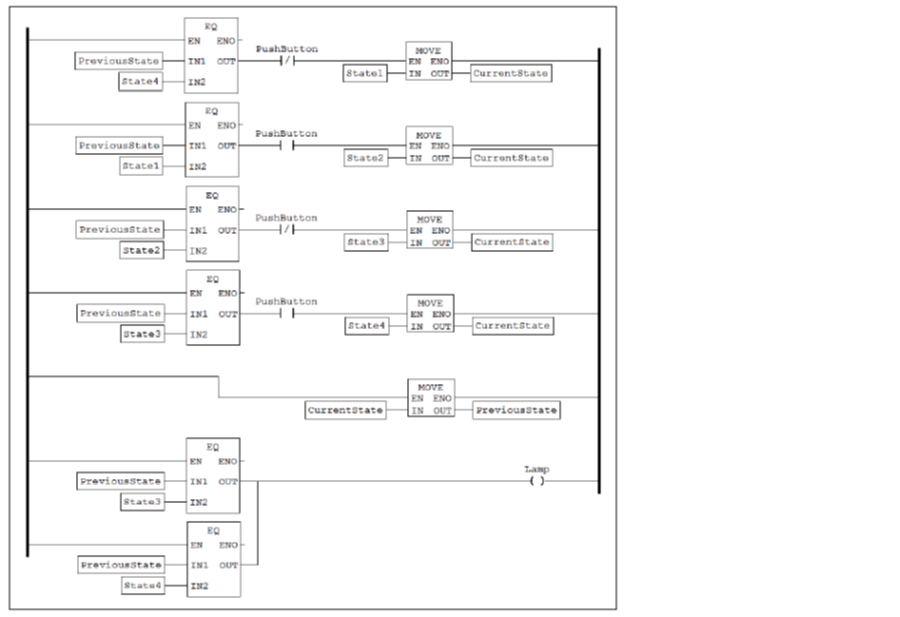
Figure 10: Ladder diagram translation of a simple toggle-on/toggle-off device
Application Example
The following sequential function chart describes a portion of a testing apparatus that performs an automated sequence of spinning an object to very high speeds. The test is performed in a covered enclosure in case the object does not pass the test.
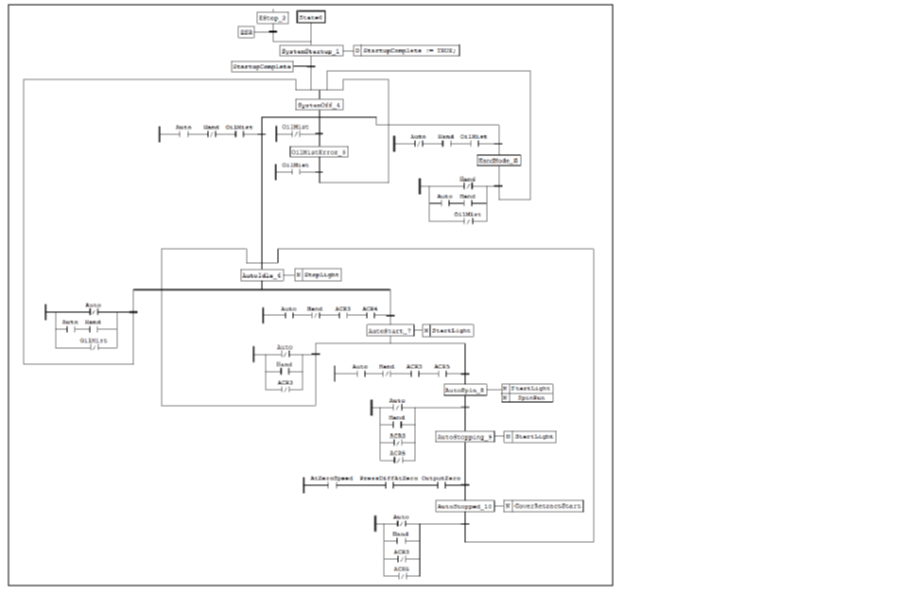
Figure 11: Sequential function chart of a test apparatus
Below are a few snapshots of the ladder diagram implemented in RSLogix500 for an Allen-Bradley SLC-500. The first illustrates the use of a first-pass system bit to initialize the current state (SM_MAIN_CS) and previous state (SM_MAIN_PS) variables. Next, the rungs for states 1 (SystemStartup), 2 (EStop), and 3 (OilMistError) are shown. State 0 shown above is just a startup state and that is taken care of by the first-pass initialization. For simplicity, the transitions are not drawn from every state to state 2 (EStop) and the rung for this state does not use any preceding state information in activation but, instead, just the e-stop input. State 4 (SystemOff) is shown in the next figure as an example of a state with many preceding states. The timer input (STARTUP_TMR/DN) that causes the transition from state 2 to state 4 implements the D-type action (time delayed) attached to state 2 and shown above.
Finally, the rung for state 10 (AutoStopped) is shown. Following the rung for state 10 is the rung that transfers the value of the current state variable to the previous state variable. Then, a couple of outputs rungs (startup timer and spin run) are shown.

Figure 12: Use of first-pass to initialize step variables on ladder diagram of test apparatus

Figure 13: Steps 1 (SystemStartup), 2 (EStop), and 3 (OilMistError) on ladder diagram of test apparatus
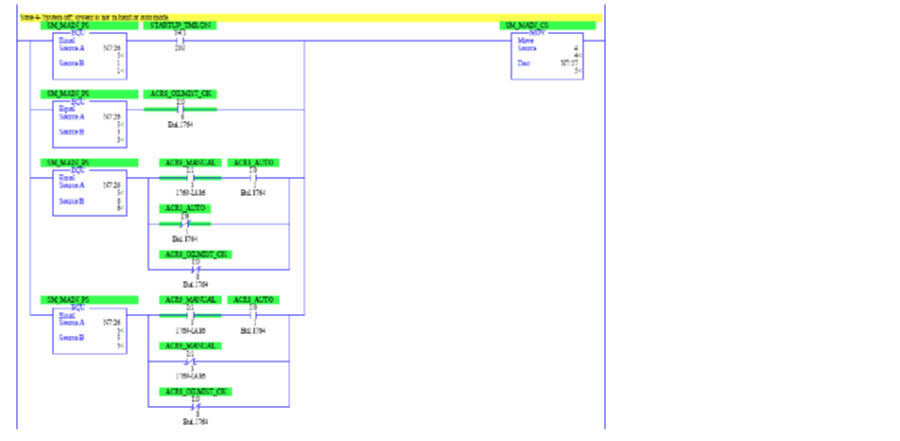
Figure 14: Step 4 (SystemOff) on ladder diagram of test apparatus
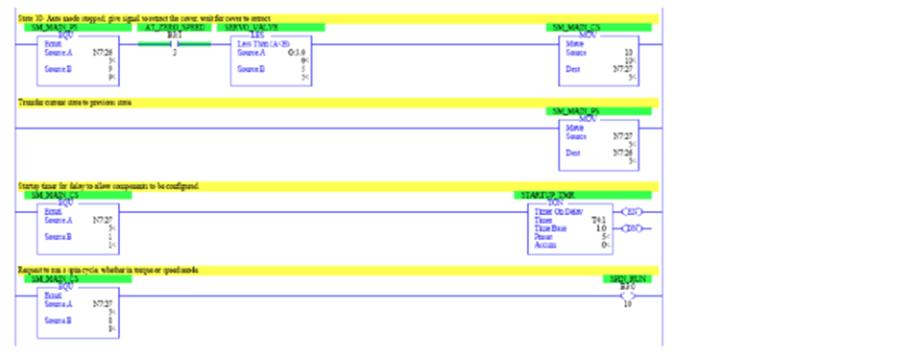
Figure 15: Step 10 (AutoStopped), step variable transfer, and example outputs on ladder diagram of test apparatus
Optimizations and Recommendations
The use of higher level PLC operations to translate sequential function charts to ladder diagrams has been useful in creating code that is easier to implement, debug, and maintain. This technique still has its flaws, though. For very large program, execution time may become large because every ladder rung is being evaluated. A majority of ladder rungs could be skipped depending on the state that is currently active. Some PLCs allow for conditional execution of ladder diagram sections and employing this strategy would be recommended.
This technique operates on Moore state machines whereas sequential function charts are truly Mealy state machines. Mealy state machines usually reduce the number of states in the system because actions are associated with inputs in addition to the active state. Altering the translation procedure for Mealy machines may require significant changes but may be worth pursuing.
Finally, this translation procedure should be automated. Manual translation, while simple and straight-forward, is very tedious. A different approach would have to be performed for each desired target hardware unless that hardware supported IEC61131-3 ladder diagrams (and not sequential function charts). Having this technique automated would facilitate using the same diagram on multiple platforms. An automatic translation procedure would also allow updates in the field to be performed more quickly.
Conclusion
While support for the IEC61131-3 standard is growing and being extended to more platforms, there are still new hardware platforms that supply little to no support for this standard and older hardware that must be reused or reprogrammed. The technique described here will allow the automation engineer to design with sequential function charts and then implement that design in the most ubiquitous PLC language, ladder diagram. Thanks to Professor Lorenz and all of the instruction at UW-Madison for teaching this technique.
Thanks also to DMC for encouraging good programming practices on a wide array of applications and hardware platforms,
Learn more about DMC's PLC Programming Servies.