What is a state machine, and why should I use one? State machines are a way of organizing code into situations, or states, and transitions so that the code is easier to follow and read. A state represents what the code and/or physical machine is currently doing, and transitions represent ways for the system to move between states. In this overview, I’ll cover some of the basics of using state machines to control industrial machines.
States
First, we should contrast the two most common types of state machines, Moore and Mealy. Moore state machines set outputs based on only the current state. By contrast, Mealy state machines set outputs according to the current state and current inputs into the system. The most significant difference is where decision logic is located within the state machine. Moore state machines place the decision logic in the transitions while Mealy state machines place the logic in the states.
Functionally both Moore and Mealy state machines can both accomplish the same tasks, the only difference is how readable the state machine will be. We'll focus on Moore state machines here, because I find them to generally be more readable in most situations.
For machine control, the controller dictates a system’s state. It’s often essential to have the controller verify that the state it’s in matches the physical system, particularly when recovering from power cycles or manual operation. Some systems do this exclusively with sensors, while others rely on the assistance of human inspection. For example, robotic arms typically have sensors that ensure the area is locked off for safety and then ask the operator to confirm that the area is clear before moving.
Another special case worth mentioning is when states have internal properties. These setpoints allow a single step to count or output a user-defined value. These properties are very useful for a system that needs to count the number of times something has happened or want to use a user-defined set point.
Transitions
Transitions connect states. Each transition has a direction and set of conditions that have the be met to transition into the next state. Once a transition's conditions are met, the state machine transitions states and begins setting outputs for the new state. Individual states can also have multiple leaving transitions, each with different conditions.

Sequencers
Sequencers are a subset of state machines that consist of states that each have only one transition. This means that sequencers do not have any logic to pick from multiple states and always execute the same states in the same order. Sequencers are some of the simplest state machines and are often used to help organize larger state machines, compressing multiple steps into a single step.

Finite State Machines
More complex state machines have branching transitions that allow the system to transition to different states depending on situational conditions. State machines are far from the only method of doing this but are one of the most structured and readable methods. This fact is a valuable and often overlooked aspect of programming. Readable code with clearly organized structure is easier and faster to commission and debug, as well as easier to add to latter logic if more functionality is needed.
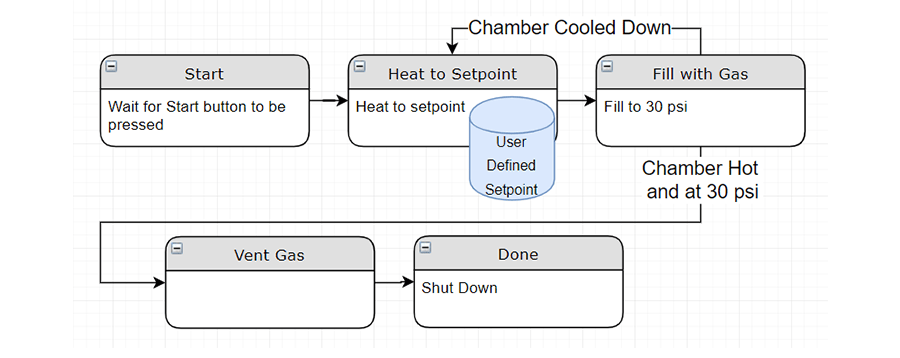
Near Infinite State Machines
More complex state machines may allow the operator to order individual steps to form more complicated processes. These state machines use an intermediate step that selects the next step based on the operator’s selection and can have near limitless configurations. The ability to define new sequences of steps on the fly and pass differing parameters to steps make these state machines, and the machines they control as versatile as possible.
Each step in the process is treated as a single state, even if functionally, it has many individual steps within it. Each step is treated as a single date because these states have only one or two possible outcomes: successful completion and/or unsuccessful completion. When a step is completed successfully, the systems will execute the next step, and so on until all the defined steps are complete. If a step fails, the system will transition to a fault handling state, pausing the machine and communicating the error to the operator.
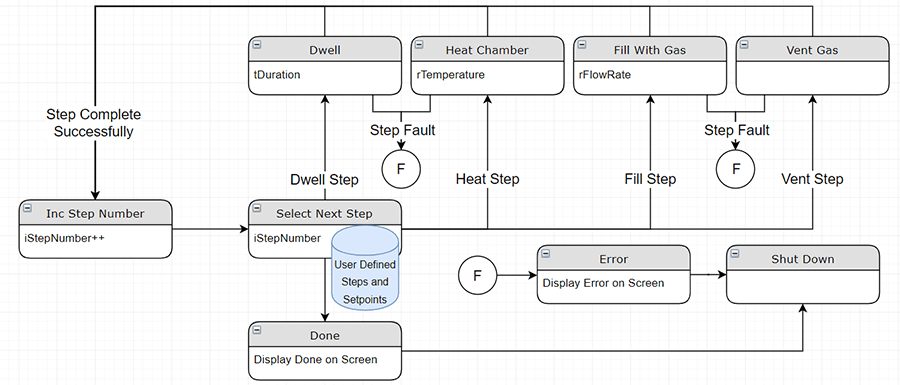
The difficulty in designing this type of state machine and still making it easy to use lies in structuring each step so that it can follow any other step. Special care must be taken to disable or prevent potentially dangerous actions from executing when they could cause damage to the machine or operator.
Hopefully, this information helps you understand a little more about how state machines and the systems they control work. Developing a proper state machine early on can save a lot of time and effort, as well as preventing a costly bug in the program. Also if you’re programming in Siemens’ TIA Portal, check out the Sequencer block in the Siemens Open Library, it’s great for designing sequences and state machines.
Learn more about our PLC Programming expertise. Contact us for any project inquiries.